23 引力场和质量的定义方程

黄色表示原文中的重点语句; 红色表示 "新增配图" 或者 "对原文细节错误进行修正"; 蓝色表示我自己的一些见解; 绿色表示一些疑问;

在统一场论中，物体 \(o\) 点的质量 \(m\) ，表示了 \(o\) 点周围 \(4\pi\) 立体角度内以光速、以圆柱状螺旋式发散运动空间位移 \(\vec{r}\) 的条数。

\(o\) 点在周围产生的引力场 \(\vec{A}\) ，表示了穿过包围 \(o\) 点的高斯球面 \(s\) 上，以光速发散运动的空间位移的条数。

"高斯球面" (Gaussian surface) 是在矢量场分析中的一个重要概念，它是一个假想的封闭曲面。在这里，具体是指围绕质点 \(o\) 的一个球形封闭曲面，可以是任意半径。这个球面用于计算通过它的空间位移通量。

引力场的定义方程：

设想有一个质点 \(o\) 相对于我们观测者静止，周围空间中任意一个空间点 \(p\)，在零时刻以矢量光速度 \(\vec{c}\) 从 \(o\) 点出发，以圆柱状螺旋式沿某一个方向运动，经历了时间 \(t\)，在 \(t'\) 时刻到达 \(p\) 后来所在的位置。

我们让点 \(o\) 处于直角坐标系 \(xyz\) 的原点，由 \(o\) 点指向 \(p\) 点的矢径 \(\vec{r}\) 由前面的时空同一化方程 \(\vec{r}(t) = \vec{c}t = x\vec{i} + y\vec{j} + z\vec{k}\) 给出，\(\vec{r}\) 是空间位置 \(x, y, z\) 和时间 \(t\) 的函数，随 \(x, y, z, t\) 的变化而变化，记为：

\[ \begin{equation}\nonumber \vec{r} = \vec{r}(x, y, z, t) \end{equation} \]

此处公式有待修正. 原著中 19 螺旋时空波动方程 已经修正了, 如下图所示; 但这里似乎还没有. 这里将 \(\vec{r}\) 写成一个关于 \(x, y, z, t\) 的四元函数, 将时间 \(t\) 看作了第四个维度, 让人感觉和统一场论的时空同一性背道而驰, 反而是降维到了相对论的四维时空观. 但这里无需纠结这一问题, 因为不影响本章内容的理解.

注意，\(p\) 点在空间中走过的轨迹是圆柱状螺旋式，我们也可以认为是矢径 \(\vec{r}\) 的一个端点 \(o\) 不动，另一个端点 \(p\) 运动变化，使得 \(\vec{r}\) 在空间中划过一条圆柱状螺旋式轨迹。

我们以 \(\vec{r} = \vec{c}t\) 中 \(\vec{r}\) 的标量长度 \(r\) 为半径，作高斯球面 \(s = 4 \pi r^2\)【在普遍情况下，高斯球面可以不是一个正球面，但是，球面是连续的、不能有破洞】包围质点 \(o\)。

我们把高斯球面 \(s = 4 \pi r^2\) 均匀的分割成许多小块，我们选择 \(p\) 点所在的一小块矢量面元 \(\Delta\vec{S}\)【 \(\Delta\vec{S}\) 方向我们用 \(\vec{N}\) 来表示，其数量为曲面 \(\Delta{S}\) 】，我们考察发现 \(\Delta{S}\) 上有 \(\Delta{n}\) 条类似于 \(p\) 的空间点的位移矢量 \(\vec{r}\) 垂直的穿过。

注意：高斯球面 \(s\) 的半径也可以不等于 \(\vec{r}\) 的标量长度，我们设定是相等的，好处是使考察点 \(p\) 恰巧落在高斯球面 \(s\) 上。

这样，\(o\) 点在空间点 \(p\) 处产生的引力场 \(\vec{A}\)【数量为 \(A\)】: \[ \begin{equation}\nonumber A = 常数乘以 \frac{\Delta{n}}{\Delta{S}} \end{equation} \]

上式实际上是定义了引力场强度的数量公式: "引力场强度" 的大小, 就等于 "空间位移密度". 这与目前大学物理教材中, 给出的 "电场强度" 就等于 "电场线密度" 类似: (以下内容截取自马文蔚物理学(第六版)上册p172)

上式给出的引力场定义简单明了，但过于粗糙，不能把引力场矢量性质表现出来，也没有把以矢量光速运动的空间位移 \(\vec{r}\) 带进式子中去。

为了达到以上目的，我们主要考察 \(p\) 点周围情况。

\(p\) 点的矢量位移 \(\vec{r} = \vec{c}t\) 垂直的穿过 \(\Delta\vec{S}\) ，普遍情况下，矢量位移 \(\vec{r} = \vec{c}t\) 可以不是垂直的穿过 \(\Delta\vec{S}\)，可以和矢量面元 \(\Delta\vec{S}\) 的法方向 \(\vec{N}\) 有一个夹角 \(\theta\)。

在 \(o\) 点相对于我们观察者静止，\(o\) 点周围空间的运动是均匀的，没有那个方向是特殊的，而且，我们使用的高斯球面是一个正圆球面，在这些条件限制下，矢量 \(\vec{r} = \vec{c}t\) 才是垂直穿过矢量面元 \(\Delta\vec{S}\)

这样，\(o\) 点在周围空间 \(p\) 点处产生的引力场 \(\vec{A}\)【矢量形式】可以写为： \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} \end{equation} \] 式中 \(G\) 是万有引力常数，\(k\) 是比例常数。注意，引力场 \(\vec{A}\) 和由 \(o\) 点指向空间点 \(p\) 的位矢 \(\vec{r}\) 方向相反。

设想 \(o\) 点周围有 \(n\) 条类似于 \(\vec{r}\) 的空间位移矢量，以 \(o\) 点为中心，呈辐射状分布，但是，任意两条的方向都不一样。

而 \(n\) 乘以 \(\vec{r}\) 即 \(n\vec{r}\) 的物理意义表示 \(n\) 条空间位移的方向都是一样的，叠加在一起。

所以，当以上的 \(\vec{r}\) 为矢量，只有 \(\Delta{n}=1\) 的情况下，才具有物理意义。但是，我们要注意 \(n\) 乘以 \(r\)【\(r\) 是 \(\vec{r}\) 的数量】中，当 \(n\) 是大于1的整数仍然具有物理意义。

所以有式： \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} = - \frac{G\ k\ \vec{r}}{\Delta{S}\ r} \end{equation} \]

我对上面这段论述有极大的疑惑: "因为只有 \(\Delta{n}=1\) 的情况下公式才具有物理意义, 所以 \(\Delta{n}\) 就直接等于1". 这肯定是有问题的.

按照我的理解, 应该写为:

\[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} = - \frac{G\ k\ \vec{r}}{\frac{\Delta{S}}{\Delta{n}}\ r} \end{equation} \]

我认为原著公式中第三个式子 (\(- \frac{G\ k\ \vec{r}}{\Delta{S}\ r}\)) 中的 \(\Delta{S}\), 其实表达的是 "单位条数对应的面积", 和第二个式子 (\(- \frac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r}\)) 中的 \(\Delta{S}\) 其实是不同的, 但作者用了同一个字母表达它们. 而且很乱的一点是, 这里明明舍弃了 \(\Delta{n}\), 但是下面依然频繁出现 \(\Delta{n}\). 

上式中为什么用 \(\vec{r}\) 的单位矢量 \(\frac{\vec{r}}{c}\)，而不是直接用矢量 \(\vec{r}\) ？

是因为我们在高斯球面 \(s\) 上只能考察矢量 \(\vec{r}\) 的方向和条数，而不能考察矢量 \(\vec{r}\) 的长度，所以 \(\frac{\Delta{n}\ \vec{r}}{\Delta{S}}\) 这个式子其实是没有物理意义的。

如果 \(\vec{r}\) 不完全是垂直穿过矢量面元 \(\Delta\vec{S}\)【数量为 \(\Delta{S}\) 】，和矢量面元的法方向 \(\vec{N}\) 具有一个角度 \(\theta\)，当空间点的位移 \(\vec{r}\) 的条数 \(n\) 设定为1的时候，以上方程也可以用矢量点乘公式来表示。 \[ \begin{equation}\nonumber \vec{A} \cdot \Delta \vec{S} = - A\ \Delta S\ cos\theta = -G\ k\ \Delta n \end{equation} \]

校正公式: 上述公式最后一个式子似乎少乘了一个 \(cos \theta\); 即最后一个式子应为: \(-G\ k\ \Delta n\ cos \theta\)

上式中 \(A\) 是引力场 \(\vec{A}\) 的数量。

引力场 \(\vec{A}\) 是由大小和方向余弦两个量决定的。

大小是指光速运动空间位移 \(\vec{r}\) 在高斯球面 \(s\) 上分布的密度（\(\frac{1}{\Delta S}\) )。

\(\frac{1}{\Delta S}\) 或者 \(\frac{\Delta n}{\Delta S}\) 表示了含两个自变量的函数，随 \(\Delta n\) 和 \(\Delta S\) 变化而变化。

方向余弦是 \(\Delta\vec{S}\) 的法方向 \(\vec{N}\) 和 \(\vec{r}\) 的夹角 \(\theta\) 的余弦，也就是 \(cos \theta\)。

方向余弦 \(cos \theta\) 是只含一个自变量的函数，这个函数随 \(\theta\) 变化而变化。

式 \[ \begin{equation}\nonumber A = 常数乘以 \frac{\Delta{n}}{\Delta{S}} \end{equation} \] 和 \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} \end{equation} \]

这两个式子的物理意义告诉我们：

高斯球面 \(s = 4 \pi r^²\) 其中一小块矢量面元 \(\Delta\vec{S}\) 上，垂直穿过空间矢量位移 \(\vec{r}\)【 \(\vec{r} = \vec{c}t\) 】的密度反映了该处的引力场强度。

我们将式 \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} \end{equation} \]

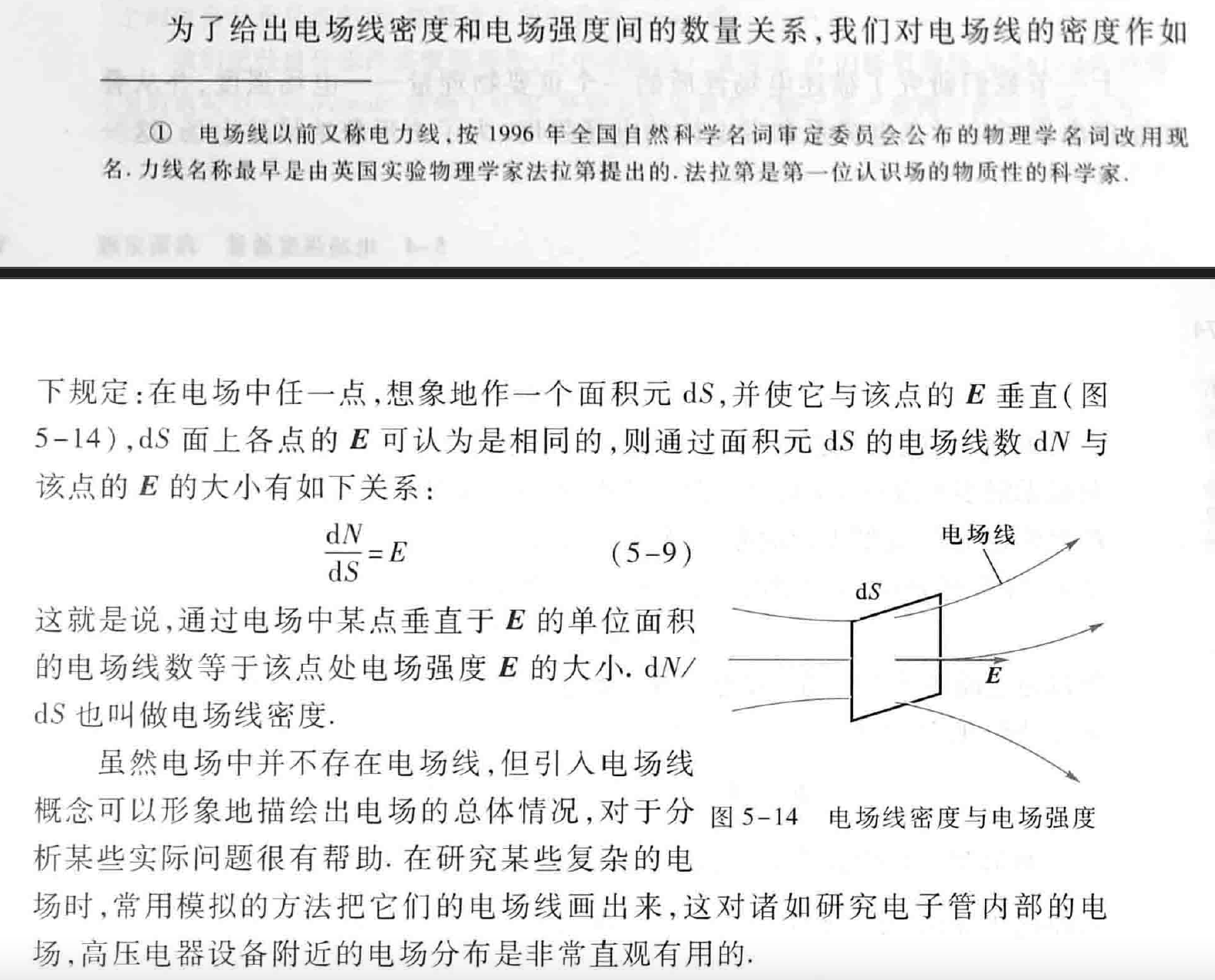
中的 \(\Delta S\) 用立体角 \(\Omega\) 和高斯球面的半径 \(r\) 来表示，也就是 \(\Delta S = \Omega\ r^2\) \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^2\ r} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation} \]

上图中，我们将高斯球面中的一小块矢量面元 \(\Delta S\) 用 \(dS\) 表示。则： \[ \begin{equation}\nonumber dS = r\ d\theta\ r\ sin\theta\ d\varphi = r^2\ d\theta\ sin\theta\ d\varphi = r^2\ d\Omega \end{equation} \]

质量的定义方程

质量的本质是什么？质量和引力场是什么关系？

由于质量的概念起源于牛顿力学，我们把以上统一场论引力场几何形式的定义方程 \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation} \] 和牛顿力学引力场方程 \(\vec{A} = -\frac{G\ m\ \vec{r}}{r^3}\) 相比较，可以得出物体 \(o\) 点的质量定义方程应该是: \[ \begin{equation}\nonumber m = \frac{k\ \Delta n}{\Omega} \end{equation} \] 微分式为： \[ \begin{equation}\nonumber m = \frac{k\ dn}{d\Omega} \end{equation} \] 上式 \(k\) 是常数。由于空间可以无限分割，所以，以上的 \(n\) 的微分，也就是 \(dn\) 是有意义的。

对上式右边环绕积分，积分区域在 \(0\) 和 \(4 \pi\) 之间，则： \[ \begin{equation}\nonumber m = k\ \frac{\oiint dn}{\oiint d\Omega} = k\ \frac{n}{4\pi} \end{equation} \] 上式的物理意义是：

\(o\) 点的质量 \(m\) 表示周围立体角 \(4\pi\) 内分布有 \(n\) 条空间位移矢量 \(\vec{r} = \vec{c}t\)

以上 \[ \begin{equation}\nonumber m = \frac{k\ dn}{d\Omega} \end{equation} \]

是质量的几何形式的微分定义方程。

在很多种情况下，我们将 \(n\) 设定为1，可以得到质量的简化定义方程： \[ \begin{equation}\nonumber m = \frac{k}{\Omega} \end{equation} \]

注意上式中 \(\Omega\) 的含义也会发生变化; 变成 "单位空间位移对应的立体角" 了. 原著中经常有类似的地方, 用同一个字母表达多个含义; 明白其意思就好.

我们一旦知道了质量的本质，就可以对牛顿力学中的引力场方程 \(\vec{A} = -\frac{G\ m\ \vec{r}}{r^3}\) 做出解释。

按照牛顿力学，我们以地球【用 \(o\) 点表示，我们观察者站在地球上】为例，地球上空一个卫星【用 \(p\) 点表示】，由 \(o\) 点指向 \(p\) 点的位置矢量【间称位矢】用 \(\vec{r}\)【数量为\(r\)】表示。

则 \(o\) 点在 \(p\) 点处产生的引力场 \(\vec{A} = -\frac{G\ m\ \vec{r}}{r^3}\)， 表示在以半径为 \(r\) 的高斯球面 \(s = 4 \pi r^2\) 上，分割了一小块矢量面元 \(\Delta\vec{S}\)，\(\Delta\vec{S}\) 上穿过了1条矢量 \(\vec{r}\) ，并且， \(\vec{r}\) 和 \(\vec{A}\) 方向相反。

\(\Delta\vec{S}\) 的数量 \(\Delta{S}\) 的倒数反映了引力场的大小，\(\Delta\vec{S}\) 的反方向就是引力场的方向。

我们需要注意的是，统一场论的引力场方程，反映了某一个瞬间，或者是某一个时刻的情况。

对统一场论的静止引力场 \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation} \] 求旋度，在 \(\Delta n\) 和 \(\Omega\) 是常数【也就是质量为常数】的情况下，仅 \(\frac{\vec{r}}{r^3}\) 是变量，结果为零： \[ \begin{equation}\nonumber \vec{\nabla} \times \vec{A} = \vec{0} \end{equation} \] 这里的 \(\vec{\nabla}\) 叫做向量微分算子. 对于一般的向量场: \(\vec{A}(x, y, z) = P(x, y, z)\vec{i} + Q(x, y, z)\vec{j} + R(x, y, z)\vec{k}\), \((\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z})\vec{i} + (\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x})\vec{j} + (\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y})\vec{k}\) 叫做向量场 \(\vec{A}\) 的旋度, 记作 \(\overrightarrow{\textup{rot}}\ \vec{A}\). 并且有 \(\overrightarrow{\textup{rot}} \vec{A} = \vec{\nabla} \times \vec{A}\) (摘自同济大学高等数学第七版下册p246)< /span>

对静止引力场 \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation} \] 求散度，在（ \(m = \frac{k\ \Delta n}{\Omega}\) ）是常数的情况下，仅 \(\frac{\vec{r}}{r^3}\) 是变量，结果也为零： \[ \begin{equation}\nonumber \vec{\nabla} \cdot \vec{A} = 0 \end{equation} \] 对于一般的向量场: \(\vec{A}(x, y, z) = P(x, y, z)\vec{i} + Q(x, y, z)\vec{j} + R(x, y, z)\vec{k}\), \(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}\) 叫做向量场 \(\vec{A}\) 的散度, 记作 \(\textup{div}\ \vec{A}\). 并且有 \(\textup{div}\ \vec{A} = \vec{\nabla} \cdot \vec{A} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}\) (摘自同济大学高等数学第七版下册p238)< /span>

但在 \(r\) 趋近于零【也可以说空间点 \(p\) 无限趋近于 \(o\) 点】，且 \(o\) 点可以看成一个无限小的球体的情况下，式子出现了0/0的情况，利用狄拉克 \(\delta\) 函数，可以得到： \[ \begin{equation}\nonumber \vec{\nabla} \cdot \vec{A} = 4 \pi\ G\ u \end{equation} \]

\(G\) 是万有引力常数，\(u = \frac{m}{\Delta x \Delta y \Delta z}\) 是物体 \(o\) 点的密度。

统一场论给出的引力场定义方程的旋度和散度，和牛顿力学给出的引力场的散度、旋度是一致的。

肯定是一致的, 因为统一场论给出的引力场定义方程, 相比于牛顿力学, 只是进一步将质量 \(m\) 展开为 \(\frac{k\ \Delta n}{\Omega}\), 而上述推导都假设 \(m\) 不变, 将其视作常数.

从质量定义方程导出相对论质速关系

相对论用动量守恒和相对论速度变换公式，可以导出相对论质速关系——质量随物体运动速度增大而增大。

相对论又用质速关系推导出相对论质能方程，所以，质速关系很重要。

下面我们用质量的定义方程直接导出质速关系。

设想一个质量为 \(m’\) 的质点 \(o\) ，一直静止在 \(s’\) 系的坐标原点 \(o’\) 上。

\(s\) 系相对于 \(s’\) 系以匀速度 \(\vec{v}\)【标量为 \(v\) 】沿 \(x\) 轴正方向运动，并且 \(s\) 系的 \(x\) 轴和 \(s’\) 系的 \(x’\) 轴相互重合。

在 \(s\) 系里的观察者看来 \(o\) 点的质量为 \(m\)，我们用以上的质量几何定义方程 \(m \oiint d\Omega = k\ \oiint dn\) 来求出 \(\vec{v}\) 和 \(m\)、\(m’\) 之间满足的数学关系。

当 \(o\) 点运动的时候，我们应该合理的认为，不会引起空间点矢量位移 \(\vec{r}\) 的条数 \(n\) 的变化，只是有可能引起立体角度 \(\Omega\) 的变化。所以，我们只要求出运动速度 \(\vec{v}\) 和 \(\Omega\) 之间满足的关系，也就是 \(\Omega\) 的相对论变换，就可以求出 \(m’\) 和 \(m\) 之间的关系。

立体角 \(\Omega\) 的定义为：

在以 \(o\) 点为球心、半径 \(r = 1\) 的球面 \(s\) 上，分割一小块 \(\Delta s\)，以 \(\Delta s\) 为底面，以 \(o\) 点为顶点，构成一个圆锥体 \(h\)，则 \(\Delta s\) 等于圆锥体h的立体角。

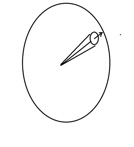
锥体 \(h\) 的立体角 \(\Omega\) 大小为锥体的底面积 \(\Delta S\) 与球的半径 \(r\) 平方之比，当 \(\Delta S\) 无限的小，变成了 \(dS\)，有： \[ \begin{equation}\nonumber d\Omega = \frac{dS}{r^2} \end{equation} \] 当 \(r = 1\) 时候，上式变成了 \(d\Omega = dS\)

以上是用锥体的底面积来定义立体角，现在我们把以上的立体角定义推广，用锥体的体积来定义立体角。

在以 \(o\) 点为球心、半径 \(r = 1\) 的球面 \(s\) 上，分割一小块 \(\Delta S\) ，以 \(\Delta S\) 为底面，以 \(o\) 点为顶点，构成一个圆锥体 \(h\)，则圆锥体 \(h\) 的体积 \(\Delta V\) 等于圆锥体 \(h\) 的立体角。

圆锥体 \(h\) 的立体角 \(\Omega\) 大小为锥体的体积 \(\Delta V\) 与球的半径 \(r\) 立方之比，当 \(\Delta V\) 无限的小，变成了 \(dV\)，有： \[ \begin{equation}\nonumber d\Omega = \frac{dV}{r^3} \end{equation} \] > 疑问: 由于 \(\Delta V = \frac{1}{3}\Delta S\ r\), 所以上面的公式是否应该修正成 \(d\Omega = \frac{3\ dV}{r^3}\) ?

当 \(r = 1\) 时候，上式变成了 \[ \begin{equation}\nonumber d\Omega = dV \end{equation} \] > 疑问: 是否应该修正成 \(d\Omega = 3\ dV\) ?

有了以上的准备知识，我们来考虑以上的 \(o\) 点在 \(s’\) 系里，静止时候质量 \[ \begin{equation}\nonumber m' = k\ \frac{\oiint dn}{\oiint d\Omega'} \end{equation} \] 我们用一个半径为1的单位球体积，在其中分割一个顶点在球心 \(o\) 点上、体积为 \(dv’\) 的圆锥体，替代上式中的 \(d\Omega’\)，则： \[ \begin{equation}\nonumber m' = k\ \frac{\oiint dn}{\oiint dv'} \end{equation} \] 相应的在 \(s\) 系里，\(o\) 点以速度 \(\vec{v}\)【标量为 \(v\)】匀速直线运动的时候，质量 \[ \begin{equation}\nonumber m = k\ \frac{\oiint dn}{\oiint dv} \end{equation} \] 注意，\(n\) 在 \(s’\) 系和 \(s\) 系里是一样的，也就是 \(o\) 点的运动速度 \(\vec{v}\) 不能改变几何点位移的条数 \(n\)。

我们只要求出 \(dv’= dx’\ dy’\ dz’\) 和 \(dv = dx\ dy\ dz\) 之间的关系，就可以求出 \(m\) 和 \(m’\) 之间的关系。

根据相对论中的最简版洛伦兹正变换【因为我们默认了观察者我在 \(s\) 系里，质点 \(o\) 相对于我在运动】： \[ \begin{align} x' &= \frac{x - vt}{\sqrt{1 - \frac{v^2}{c^2}}}\nonumber \\ y' &= y\nonumber \\ z' &= z\nonumber \\ t' &= \frac{t - \frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}\nonumber \end{align} \] 在最简版洛伦兹变换中，由于考察点 \(o\) 点在 \(s’\) 系中的位置 \(x’\) 是静止的，在 \(s\) 系里是以速度 \(\vec{v}\) 运动。

我们只有把 \(s\) 系里的时间 \(t\) 取一个固定的时刻，\(x\) 和 \(x’\) 相互比较才有意义，所以，\(dt/dx=0\)，得出微分式：

上面这句解释并没有完全说清楚为什么 \(dt/dx=0\)

\[ \begin{align} dx' &= \frac{dx}{\sqrt{1-\frac{v^2}{c^2}}} \nonumber \\ dy' &= dy \nonumber \\ dz' &= dz \nonumber \end{align} \]

由此得出： \[ \begin{align} m' &= k\ \frac{\oiint dn}{\oiint dv'} = k\ \frac{\oiint dn}{\oiint dx'\ dy'\ dz'} \nonumber \\ m &= k\ \frac{\oiint dn}{\oiint dv} = k\ \frac{\oiint dn}{\oiint dx\ dy\ dz} \nonumber \end{align} \] 由 \(\oiint dx'\ dy'\ dz' = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\oiint dx\ dy\ dz\)

可以导出： \[ \begin{equation}\nonumber m = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} m' \end{equation} \] 当 \(o\) 点以速度 \(\vec{v}\) 运动的时候，质量增大了一个相对论因子 \(\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)，这个结果和相对论是一致的。

引力场的洛伦兹变换

有了引力场和质量的定义方程，质速关系方程，加上相对论的洛伦兹变换，就可以导出引力场在两个相互匀速直线运动的参考系 \(s’\) 系和 \(s\) 系之间的变换。

设想惯性参考系 \(s’\) 相对于 \(s\) 系以速度 \(\vec{v}\)【标量为 \(v\)】沿 \(x\) 轴匀速直线运动运动。在 \(s’\) 系里，一个静止的很薄的矩形面板，带有质量，在薄板上面产生引力场 \(\vec{A'}\)

我们让薄板垂直于 \(x\) 轴，

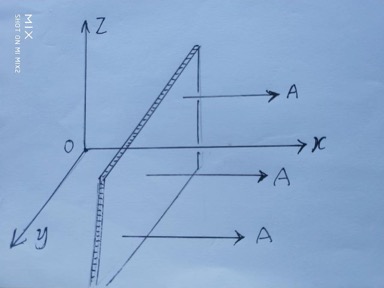
那么在 \(s\) 系里的观察者看来，引力场 \(\vec{A}\) 沿 \(x\) 轴的分量 \(A_x\) 似乎不会变化。

因为前面的引力场定义方程告诉我们，引力场强度与 垂直 穿过曲面上 单位面积的 空间位移的条数成正比，也就是与密度成正比。这里的薄板的面积没有变化，条数不会变化，密度也就没有变化。

但是，薄板的质量增大了一个相对论因子 \(\sqrt{1-\frac{v^2}{c^2}}\)

校正: 这里应该是想说质量增大了一个相对论因子\(\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)

质量的增大，从几何角度看，应该是空间位移矢量方向与考察的立体角之间的对应变化，所以： \[ \begin{equation}\nonumber A_x = \frac{A_x'}{\sqrt{1-\frac{v^2}{c^2}}} \end{equation} \] \(A_x'\) 为 \(s’\) 系里引力场 \(\vec{A'}\) 的沿 \(x’\) 轴上的分量。

当我们把薄板和 \(x\) 轴平行，

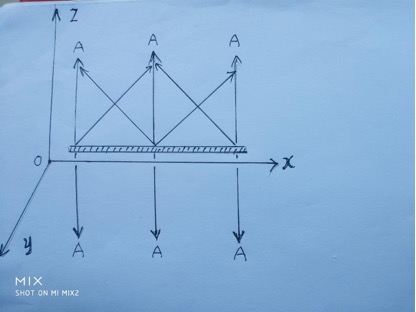
薄板要收缩一个相对论因子，加上质量增大一个相对论因子。注意，图中倾斜的引力场线在 \(x\) 轴上的投影的分量正反相互抵消为零。所以，我们得到了： \[ \begin{align} A_x &= 0 \nonumber \\ A_y &= \frac{A_y'}{1-\frac{v^2}{c^2}} \nonumber \\ A_z &= \frac{A_z'}{1-\frac{v^2}{c^2}} \nonumber \end{align} \] \(A_y'\) 和 \(A_z'\) 是 \(s’\) 系里引力场 \(\vec{A'}\) 在 \(y’\) 轴和 \(z’\) 轴上两个分量。

由前面的引力场定义方程，我们得到： \[ \begin{align} A_x' &= - \frac{G m' x'}{(r')^3} \nonumber \\ A_y' &= - \frac{G m' y'}{(r')^3} \nonumber \\ A_z' &= - \frac{G m' z'}{(r')^3} \nonumber \end{align} \] 由此导出： \[ \begin{align} A_x &= - \frac{G\ m'\ x'}{\sqrt{1-\frac{v^2}{c^2}}\ {r'}^3} \nonumber \\ A_y &= - \frac{G\ m'\ y'}{(1-\frac{v^2}{c^2})\ {r'}^3} \nonumber \\ A_z &= - \frac{G\ m'\ z'}{(1-\frac{v^2}{c^2})\ {r'}^3} \nonumber \end{align} \] 由此得到： \[ \begin{align} A_x &= - G\ m\ \gamma\ \frac{x - vt}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \nonumber \\ A_y &= - G\ m\ \gamma\ \frac{y}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \nonumber \\ A_z &= - G\ m\ \gamma\ \frac{z}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \nonumber \end{align} \] 由此得到： \[ \begin{equation}\nonumber \vec{A} = - G\ m\ \gamma\ \frac{(x - vt)\vec{i} + y\vec{j} + z\vec{k}}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \end{equation} \]

令 \(\theta\) 为矢径 \(\vec{r}\)【标量为 \(r = \sqrt{\gamma^2(x-vt)^2+y^2+z^2}\) 】和速度 \(\vec{v}\)【标量为 \(v\)】之间的夹角，\(\vec{A}\) 可以表示为极坐标形式： \[ \begin{equation}\nonumber \vec{A} = - \frac{G\ m}{\gamma^2\ r^2(1 - \beta^2\ sin^2\theta)^{\frac{3}{2}}}\ \vec{e_r} \end{equation} \] 式中 \(G\) 为万有引力常数, \(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\) ，\(\beta = \frac{v}{c}\)，\(\vec{e_r}\) 是矢径 \(\vec{r}\)（标量为 \(r\) )的单位矢量。

这个结果和电场的相对论变换形式是一样，这个表明，高斯定理适用于静止引力场，也适用于匀速直线运动的引力场。

在 \(s’\) 系里有， \[ \begin{equation}\nonumber \vec{\nabla} \cdot \vec{A'} = \frac{\partial{A_x'}}{\partial{x'}} + \frac{\partial{A_y'}}{\partial{y'}} + \frac{\partial{A_z'}}{\partial{z'}} = \frac{G\ m'}{dV'} \end{equation} \] 在 \(s\) 系里有： \[ \begin{equation}\nonumber \vec{\nabla} \cdot \vec{A} = \frac{\partial{A_x}}{\partial{x}} + \frac{\partial{A_y}}{\partial{y}} + \frac{\partial{A_z}}{\partial{z}} = \frac{G\ m}{dV} \end{equation} \] 其中 \(G\) 是万有引力常数，\(s’\) 系里的 \(dV' = dx'\ dy'\ dz'\) ，质量为 \(m’\)， \(s\) 系里的 \(dV = dx\ dy\ dz\)，质量为 \(m\)。

由以上的引力场变换，可以证明这两个高斯公式都能够成立，高斯定理不仅适用于静止物体的静止引力场，同样适用于运动物体的引力场。

注意，式中 \(\gamma dx = dx’\) 是从洛伦兹正变换 \(x’ = \gamma(x - v t)\) 求微分得到的。

和之前一样, 这里直接将 \(dt\) 那一项丢掉了