30 电荷与电场的定义方程
黄色表示原文中的重点语句; 红色表示 "新增配图" 或者 "对原文细节错误进行修正"; 蓝色表示我自己的一些见解; 绿色表示一些疑问;
电荷的定义方程
在统一场论中,电荷和质量都是质点周围空间以光速、以圆柱状螺旋式向四周发散运动的运动效应,二者有一个共同的起源——空间的光速、螺旋发散运动。
设想质点 \(o\) 相对于我们观察者静止,由 \(o\) 点指向周围一个空间点 \(p\) 点的位矢为 \(\vec{r}\) ,我们以 \(\vec{r}\) 的数量 \(r\) 作一个高斯球面 \(s=4 \pi r^2\) 包围 \(o\) 点。
\(\vec{r}\) 的一个端点在 \(o\) 点上,另一个端点 \(p\) 因为是以圆柱状螺旋式运动,其中的旋转运动会在高斯面 \(s\) 上画出一个立体角 \(\Omega\) 。
前面指出,\(o\) 点带有质量 \(m\) 可以表示为:
\[ \begin{equation}\nonumber m = k\ \dfrac{1}{\Omega} \end{equation} \]
质量 \(m\) 表示包围 \(o\) 点的立体角 \(4\pi\) 内,穿过了 \(n\) 条光速运动空间位移矢量 \(\vec{r}\)
式 \(m = k\ \dfrac{1}{\Omega}\) 是质量定义方程的简化,表示在单位立体角 \(\Omega\) 上恰巧有一条 \(\vec{r}\)
点击展开修正:「 表示在单位立体角 \(\Omega\) 上恰巧有一条 \(\vec{r}\) 」这句话似乎存在问题
在统一场论中,质点 \(o\) 如果带有电荷 \(q\) ,\(q\) 表示单位时间里、单位立体角上穿过的 \(\vec{r}\) 的条数。也就是质量 \(m\) 随时间 \(t\) 变化的变化程度就是电荷,所以,有电荷的定义方程:
\[ \begin{equation}\nonumber q = k'\ \dfrac{dm}{dt} = -\ k'\ k\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt} \end{equation} \]
式中 \(k'\) 为常数。
以上就是电荷的微分定义方程,也可以认为是电荷的几何形式定义方程。
这个电荷定义方程,反映了电荷的大小与质点周围空间旋转运动立体角的角速度有关。
由于 \(\Omega\) 是立体角,\(4\pi\) 是其中一个最重要的取值,这个是电荷量子化的根本原因。
\(\dfrac{d\Omega}{dt}\) 的变化是角度的变化,变化呈现往复性,所以,时间 \(t\) 的变化呈现周期性。
从这个定义式可以看出,电荷的本质与空间的旋转频率密切相关。
这里对电荷的定义,一部分是假设,一部分是推理。就是说电荷是物体粒子周围空间以光速、以圆柱状螺旋式向四周发散运动的运动程度。
我们得到这个电荷定义方程,看看和我们掌握的知识是非吻合,如果全部吻合,表明这个电荷的定义方程是正确可靠的。
这个电荷定义方程,只能适用于单个电荷粒子,对于宏观物体,里面许多正负电荷粒子,是不能直接运用的,因为宏观物体的电荷大部分正负相互抵消了。
证明电荷的相对论不变性
相对论中,电荷是不随运动速度变化的,但是,相对论没有证明。下面我们用电荷定义方程给出证明。
当物体粒子 \(o\) 点相对于我们观察者静止时候,带有电荷 \(q\) ,由以上电荷和质量的关系方程:
\[ \begin{equation}\nonumber q = k'\ \dfrac{dm}{dt} \end{equation} \]
我们很容易看出,当 \(o\) 点相对于我们观察者以速度 \(v\) 运动的时候,质量 \(m\) 和时间 \(t\)【相比较固有时间】同步增大一个相对论因子 \(\sqrt{1 - \dfrac{v^2}{c^2}}\) ,所以,\(q\) 仍然不变。
点击展开修正:上面的相对论因子应取倒数
对于电荷的定义一些我们需要注意的问题
电荷 \(q\) 的定义式中的 \(\dfrac{dm}{dt}\) ,表示出粒子的电荷量和粒子的质量变化率成正比,这个似乎与事实不相符,我们在实践中没有发现电荷粒子质量在剧烈的变化,也没有发现质量随着时间持续性的增大或者减少。
这种原因,可能是电荷粒子的质量变化是周期性变化,不是随着时间变化到无穷大。
而且,这种变化的频率可能极快,如同交流电那样,由于变化的频率很快,我们感觉不到、难以检测到变化。
以上质量定义方程 \(m = k\ \dfrac{n}{\Omega}\) 中, \(k\) 是常数,单个物体粒子,在周围没有别的粒子靠近的情况下,空间运动位移的条数 \(n\) 按理不会变化,变化是立体角 \(\Omega\) 的变化,而我们知道,立体角的变化是周期性的。
如果这种情况被证实,则量子力学中物质波,粒子具有波长、频率,很可能与这个有关。
电场的几何定义方程
相对于我们观察者静止的 \(o\) 点,带有电荷 \(q\) ,在周围空间 \(p\) 点处产生电场 \(E\) ,我们用高斯球面 \(s = 4 \pi r^2\) 包围 \(o\) 点,\(p\) 为 \(s\) 上的一个考察点,由 \(o\) 指向 \(p\) 的位矢为 \(\vec{r}\) ,这样,\(\vec{r}\) 的数量为 \(r\) 。
由库伦定理给出的电场定义方程 \(\vec{E} = \dfrac{q\ \vec{r}}{4\ \pi\ \varepsilon_0\ r^3}\) 中,\(4 \pi \varepsilon_0\) 是常数,我们不需要考虑,\(\vec{r}\) 是空间位移矢量,\(r\) 是高斯球面半径,唯一我们不清楚的是电荷 \(q\) 表示了什么意思。
一旦我们搞清楚了电荷 \(q\) 的几何意义,我们也就是彻底搞清楚了电场 \(E\) 的几何意义,所以,我们把电荷 \(q\) 的定义方程
\[ \begin{equation}\nonumber q = k'\ \dfrac{dm}{dt} = -\ k'\ k\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt} \end{equation} \]
带入到 \(\vec{E} = \dfrac{q\ \vec{r}}{4\ \pi\ \varepsilon_0\ r^3}\) 中,就给出了静电场 \(\vec{E}\) 的几何定义方程:
\[ \begin{equation}\nonumber \vec{E} = -\ \dfrac{k'\ k}{4\pi\ \varepsilon_0}\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\ \dfrac{\vec{r}}{r^3} \end{equation} \]
电场表示为单位时间里空间位移 \(\vec{r}\) 穿过高斯球面 \(s\) ,在 \(s\) 上分布的密度,比起质量就是多了时间因素。
点击展开注解:与引力场 \(\vec{A}\) 的类比
电荷粒子的电场的分向和周围空间位移一致时候,是正电场,相反是负电场。
解释库仑定律
库仑定律表述如下:
相对于我们观察者,真空中两个静止的点电荷 \(q\) (电量为 \(q\) ) 与 \(q'\)(电量为 \(q'\) )之间的作用力 \(F\) 和它们的电量的乘积成正比,和他们之间距离 \(r\) 的平方成反比,作用力的方向在它们之间的连线上。
电荷有正有负,同号电荷相互排斥,异号电荷相互吸引。数学公式为:
\[ \vec{F} = \dfrac{k\ q\ q'}{r^2}\ \vec{e_r} = \dfrac{q\ q'\ \vec{r}}{4\pi\ \varepsilon_0\ r^3} \]
其中 \(k\) 为比例常数,\(\varepsilon_0\) 为真空中的介电常数 , \(\vec{r}\) 是由 \(q\) 指向 \(q'\) 的位矢,其数量为 \(r\) ,\(\vec{e_r}\) 是沿 \(\vec{r}\) 的单位矢量。
由以上电荷、电场定义方程可知,电荷 \(q\) 在 \(q'\) 处产生的电场应该为
\[ \begin{equation}\nonumber \vec{E} = -\ \dfrac{k'\ k}{4\pi\ \varepsilon_0}\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\ \dfrac{\vec{r}}{r^3} \end{equation} \]
由于电荷 \(q' = k'\ k\ \dfrac{1}{\Omega'^2}\ \dfrac{d\Omega'}{dt'}\) 在 \(q\) 附近的 \(p\) 点出现,使电荷 \(q\) 在 \(p\) 点的电场 \(\vec{E}\) 发生了变化。
我们把这种场变化【由于场的本质是以圆柱状螺旋式运动空间,其实就是空间在运动变化】理解为 \(q\) 对 \(q'\) 的作用力,用 \(\vec{E}\) 和 \(q'\) 的乘积来表示这种变化的效果,就有以上的库伦定理。
正负电荷模型
统一场论中认定了粒子带有电荷是因为粒子周围空间本身时刻以圆柱状螺旋式运动造成的。
我们知道圆柱状螺旋式运动可以分解为旋转运动和旋转平面垂直方向直线运动。
粒子带有正电荷在周围产生正电场,是由于粒子周围空间直线运动部分相对于我们观察者以粒子为中心向四周发散运动,旋转部分以逆时针旋转,所造成的,并且满足右手螺旋。
径向速度【注意,不同于沿直线方向的运动速度,而是旋转速度叠加直线方向运动速度】是矢量光速,方向由正电荷指向无穷远处的空间。
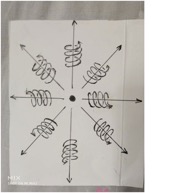
粒子带有负电荷在周围产生负电场,是由于粒子周围空间直线运动部分相对于我们观察者,从无限远处的向粒子汇聚而来,旋转部分也是逆时针,所造成的。同样满足右手螺旋。
径向速度是矢量光速,方向由无穷远处的空间指向负电荷。
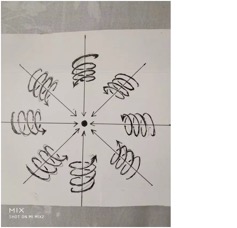
带电粒子周围空间圆柱状螺旋式是粒子带电的原因。我们知道圆柱状螺旋式运动是旋转运动和旋转平面垂直方向直线运动的叠加,我们可以用右手定则来说明。
我们在正点电荷周围作许多由正电荷指向周围空间的射线,我们用右手握住其中任意一条射线,并且大拇指和射线方向一致,则四指环绕方向就是正点电荷周围空间的旋转方向。
我们在负点电荷周围作许多由任意空间指向负电荷的射线,我们用右手手握住其中任意一条射线,并且大拇指和射线方向一致,则四指环绕方向就是负点电荷周围空间的旋转方向。
正负电荷周围空间都是右手螺旋式空间。
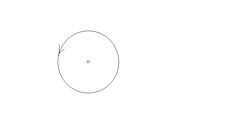
面对我们观察者,正电荷周围空间是逆时针旋转的。
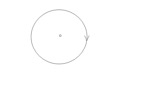
面对我们观察者,负电荷周围空间是顺时针旋转的。
以上给出的电场、电荷的定义方程,一部分是我们的假设,一部分是我们的逻辑推理。
如果这个方程和我们已经掌握的知识全部符合,则这几个定义方程就是可靠的。
我们还要注意的一点是,以上的电场、电荷的定义方程不是绝对、唯一的,我们可以根据电荷、电场的本质,给出其他形式的定义方程。
几何图形解释同种电荷排斥、异种电荷吸引
既然电荷是物体粒子周围空间圆柱状螺旋式发散运动形成的,我们能不能用一个圆柱状螺旋式运动模型来解释电荷所有的规律?
还有,等量的正电荷和负电荷碰到一起,为什么电荷会相互抵消为零?这个可以用数学严格证明吗?
答案是可以的,证明和磁场的高斯定理类似。就是用一个微小曲面 \(dS\) 去截空间圆柱状螺旋式运动的矢量位移线。
在一个有限的、大小确定的曲面上,有多少条空间位移线进去,就一定会有多少条空间位移线出来,二者相互抵消为零。把 \(dS\) 遍及包围物体粒子的高斯球面全部积分,总结果是零。
为什么正电荷和负电荷相互吸引?
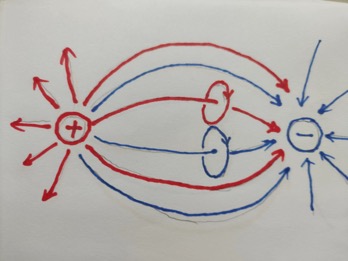
上图中,红色表示正电荷场线,蓝色表示负电场线。
带等量的正电荷和负电荷靠近,电荷周围空间的圆柱状螺旋式运动,径向部分以光速从正电荷出发,运动到负电荷结束。
空间的旋转部分相互接触的地方,由于方向相反而相互抵消。
注意,每一条电场线都带有旋转,电场线实际上是圆柱状螺旋式的,上图为了简洁,旋转线没有全部画出来。
这样正电荷和负之间的空间量在减少,有相互接触的趋势,表现为相互吸引。
两个电荷是相互离开还是相互靠近,取决于空间圆柱状螺旋式的旋转部分,因为径向方向的运动速度是光速,按照相对论,光速运动的空间缩短为零,或者说已经不属于我们所在的空间了。
一旦正电荷和负电荷极为接近,等同于一个点,周围的直线运动由于方向相反而相互抵消,旋转运动也由于方向相反而相互抵消。
这个就是等量正电荷、负电荷碰到一起,周围空间运动效应【包括静止质量】消失,电荷能够相互抵消的原因。
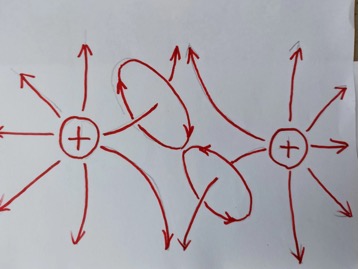
上图是两个带等量正电荷相互靠近,由于空间的旋转部分靠在一起的地方,运动方向是相同的,而使空间量加大。
注意,每一条电场线都带有旋转,电场线实际上是圆柱状螺旋式的,上图为了简洁,没有全部画出来。
这样两个正电荷之间的空间量在增加,有相互离开的趋势,表现为相互排斥。
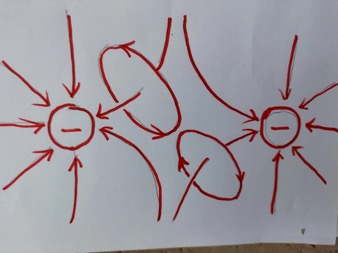
上图是两个带等量的负电荷靠近,由于空间的旋转部分靠在一起的地方,运动方向是相同的,而使空间量加大。这样两个负电荷之间的空间量在增加,有相互离开的趋势,表现为相互排斥。