33 磁场的定义方程

黄色表示原文中的重点语句; 红色表示 "新增配图" 或者 "对原文细节错误进行修正"; 蓝色表示我自己的一些见解; 绿色表示一些疑问;

在统一场论中，磁场和电场不是同一种场，二者不能直接相互作用，不能直接叠加。

人类已经发现，带电粒子相对于我们观察者以匀速直线运动的时候，可以引起电场的变化，电场变化的部分我们可以认为就是磁场，也就是随速度变化的电场产生了磁场，统一场论继承这种看法。

设想在惯性参照系 \(s'\) 系里，一个相对于我们观察者静止的 \(o\) 点，质量为 \(m'\) 【以速度 \(\vec{v}\) 运动时候为 \(m\) 】，带有正电荷 \(q\) ，在周围空间 \(p\) 【 \(p\) 点可以看成是空间点，也可以看成是场点、考察点】处产生了静电场 \(\overrightarrow{E'}\) ，【如果是负电荷，加一个负号，以速度 \(\vec{v}\) 运动时候为 \(\vec{E}\) 】，由 \(o\) 点指向 \(p\) 点的矢径为 \(\vec{r'}\) 运动时候为 \(\vec{r}\) 】。

我们以 \(\vec{r'}\) 的长度 \(r'\) 【以速度 \(\vec{v}\) 运动时候为 \(r\) 】为半径作一个高斯面 \(s' = 4 \pi {r'}^2\) 包围 \(o\) 点。

在惯性参照系 \(s\) 系里，当 \(o\) 点相对于我们以匀速度 \(\vec{v}\) 沿 \(x\) 轴直线运动的时候，可以引起 \(\vec{v}\) 垂直方向电场的变化，变化的部分我们可以认为就是磁场 \(\vec{B}\)

很简单的想法是运动电场 \(\vec{E}\) 乘以速度 \(\vec{v}\) 就是磁场 \(\vec{B}\) ，由于速度 \(\vec{v}\) 和电场 \(\vec{E}\) 相互垂直时候，产生的磁场最大，因而它们之间应该是矢量叉乘，所以有以下关系，

\[ \begin{equation}\nonumber \vec{B} = \text{常数乘以}\ (\vec{v} \times \vec{E}) \end{equation} \]

为了得到运动电场 \(\vec{E}\) 的几何形式方程，我们把由库伦定理得到的静电场定义方程

\[ \begin{equation}\nonumber \overrightarrow{E'} = \dfrac{q\ \vec{r'}}{4\pi\ \varepsilon_0\ {r'}^3} \end{equation} \]

利用洛伦兹正变换【因为电荷 \(o\) 点相对于我们观察者在运动】进行修正，可以得到：

\[ \begin{equation}\nonumber \vec{E} = \dfrac{q\ \gamma}{4\pi\ \varepsilon_0}\ \dfrac{(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \end{equation} \]

所以，

\[ \begin{equation}\nonumber \vec{v} \times \vec{E} = \dfrac{q\ \gamma}{4\pi\ \varepsilon_0}\ \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \end{equation} \]

令真空磁导率为 \(\mu_0\) ，因为我们这里讨论的是在真空情况下，则：

\[ \begin{equation}\nonumber \begin{aligned} \vec{B} &= \dfrac{\mu_0\ q\ \gamma}{4 \pi} \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \\ &= \dfrac{\mu_0\ \varepsilon_0\ q\ \gamma}{4 \pi\ \varepsilon_0} \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \\ &= \mu_0\ \varepsilon_0\ \vec{v} \times \vec{E} \end{aligned} \end{equation} \]

由于

\[ \begin{equation}\nonumber \mu_0\ \varepsilon_0 = \dfrac{1}{c^2} \end{equation} \]

所以，上式也是可以写成

\[ \vec{B} = \dfrac{1}{c^2}\ \vec{v} \times \vec{E} \]

所以，磁场的定义方程为：

\[ \begin{equation}\nonumber \begin{aligned} \vec{B} &= \dfrac{\mu_0\ q\ \gamma}{4 \pi} \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \\ &= \dfrac{\mu_0\ q\ \gamma}{4 \pi} \dfrac{v\ (-z \vec{j} + y\ \vec{k})}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \end{aligned} \end{equation} \]

上式中，人类以前一直不清楚电荷 \(q\) 是什么，现在我们一旦清楚了电荷 \(q\) 的几何形式，利用以上的电荷定义方程

\[ \begin{equation}\nonumber q = -\ k'\ k\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt} \end{equation} \]

可以得到磁场的几何形式定义方程：

\[ \begin{equation}\nonumber \vec{B} = -\ \dfrac{\mu_0\ k'\ k}{4 \pi}\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\ \gamma\ \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \end{equation} \]

令 \(\theta\) 为矢径 \(\vec{r}\) 】和速度 \(v\) 之间的夹角， \(\vec{B}\) 可以表示为极坐标形式：

\[ \begin{equation}\nonumber \vec{B} = -\ \dfrac{\mu_0\ k'\ k}{4 \pi}\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\ \dfrac{v\ sin\theta}{\gamma^2\ r^2\ (1 - \beta^2\ sin^2\theta)^\frac{3}{2}} \vec{e_r} \end{equation} \]

式中的 \(\beta = \dfrac{v}{c}\) , \(c\) 是光速， \(v\) 是 \(\vec{v}\) 的标量形式，\(\vec{e_r}\) 是矢量 \(\vec{r}\) (标量为 \(r\) ) 的单位矢量。

利用质量和电荷之间的关系 \(q = k'\ \dfrac{dm}{dt} = -\ k'\ k\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\) ，可以得到含质量的磁场定义方程：

\[ \begin{equation}\nonumber \vec{B} = \dfrac{\mu_0\ k'}{4 \pi}\ \dfrac{dm}{dt}\ \gamma\ \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \end{equation} \]

在下图中，一个相对于我们静止的带正电荷粒子 \(o\) 点，在周围空间点 \(p\) 处产生了静电场 \(\overrightarrow{E'}\) ，当 \(o\) 点相对于我们观察者以速度 \(\vec{v}\) 沿 \(x\) 轴匀速直线运动，可以产生磁场 \(\vec{B}\) 为中心轴线在旋转，\(\vec{B}\) 的旋转和 \(\vec{v}\) 满足右手螺旋关系。

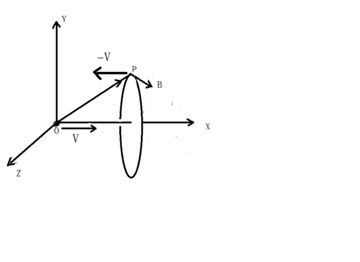
磁场 \(\vec{B}\) 和运动电场 \(\vec{E}\) 以及电荷运动速度 \(\vec{v}\) 满足以下关系：

\[ \begin{equation}\nonumber \vec{B} = \dfrac{1}{c^2}\ \vec{v} \times \vec{E} \end{equation} \]

按照矢量叉乘和斯托克斯定理排列顺序的习惯，\(y\) 叉乘以 \(z\) 形成了 \(x\) 方向上的矢量面元，\(z\) 叉乘以 \(x\) 形成了沿 \(y\) 方向的矢量面元，\(x\) 叉乘以 \(y\) 形成了沿 \(z\) 方向的矢量面元，三个分量满足以下右手螺旋关系：

\[ \begin{align} \overrightarrow{B_x} &= \vec{0} \nonumber \\ \overrightarrow{B_y} &= -\ \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_z} \nonumber \\ \overrightarrow{B_z} &= \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_y} \nonumber \end{align} \]

其中 \(\vec{v}\) 是电荷粒子 \(o\) 点沿 \(x\) 轴的的运动速度。

按照统一场论的看法，物体粒子静止时候周围空间点的运动速度是矢量光速 \(\vec{c'}\) ，当物体粒子以速度 \(\vec{v}\) 运动的时候，周围空间点的运动速度为 \(\vec{c} - \vec{v}\)

\(o\) 点静止时候，周围空间点 \(p\) 是以矢量光速 \(\vec{c'}\) 在运动，当 \(o\) 点以速度 \(\vec{v}\) 沿 \(x\) 轴直线运动的时候，\(p\) 点的矢量光速和 \(\vec{E}\) 一致，另外还叠加一个运动速度 \(-\vec{v}\) ，和 \(o\) 点运动速度 \(\vec{v}\) 正好相反。

当我们把考察点放在 \(p\) 点上，就应该把 \(o\) 点的运动速度换成空间点 \(p\) 的运动速度，以上的分量关系变成了如下左手螺旋式：

\[ \begin{align} \overrightarrow{B_x} &= \vec{0} \nonumber \\ \overrightarrow{B_y} &= \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_z} \nonumber \\ \overrightarrow{B_z} &= -\ \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_y} \nonumber \end{align} \]

当我们考察空间点 \(p\) 点的情况，用这个分量公式更直接方便。

在下图中，当电荷 \(o\) 点从 \(a\) 点开始，以匀速圆周运动到 \(b\) 点的时候，空间的旋转运动在这个圆周的正反两个面上一进一出，进的一面是 \(S\) 极，出来的一面叫 \(N\) 极。

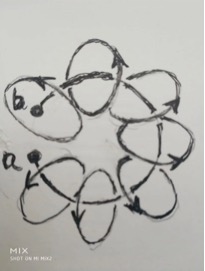
从磁场这种几何形式来看，自然界不存在有磁单极子的。