40-光子模型

发表于 2024-11-28 阅读次数： Waline：

黄色表示原文中的重点语句; 红色表示 "新增配图" 或者 "对原文细节错误进行修正"; 蓝色表示我自己的一些见解; 绿色表示一些疑问;

相对于我们观测者，加速运动的电荷会在周围空间产生加速变化的电磁场，加速变化的电磁场可以产生反引力场，反引力场可以使加速电荷、或者附近的某些电子的质量和电荷消失。

电子的质量、电荷消失，导致电子周围的力场和电磁特性消失后而激发起来，以光速向外运动，这个就是电磁波，又称光。这里有一个猜测，对于某些频率很低的电磁波，可能就是单纯的加速扭曲电磁场，其中没有包含电子这种实物粒子。

光子模型，一种是由单个激发电子相对于我们观察者以螺旋式远离我们运动，并且旋转的中心是条直线，在这个直线方向速度是光速。

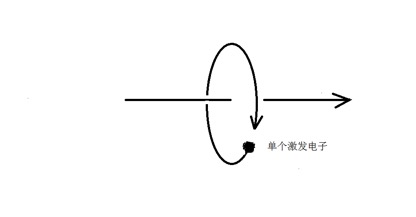
光子1.png

第二种是两个激发电子对称绕一条直线旋转，同时又沿着这条直线方向以光速运动，结果也是以圆柱状螺旋式远离我们观察者运动。

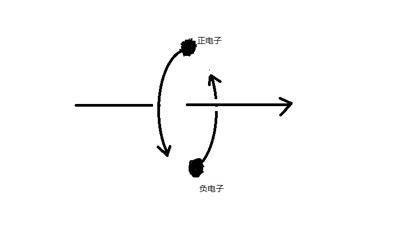
光子运动.png

电子受到了加质量力 \((\vec{c} - \vec{v})\ \dfrac{dm}{dt}\) 的作用后，处于静止质量为零的激发状态，这个就是光子，光子相对于观察者在没有改变因素的情况下始终以光速惯性运动下去。

给电子施加加质量力的能量，需要一个固定的能量可以使电子激发起来，小于这个能量，电子无法激发；大于这个能量，也无法施加到电子上，因为只要能量达到了，电子就已经激发以光速跑掉了，再加加不上了。

这个就是光子的能量是量子化的根本解释。

宇宙中任何物体粒子周围空间以粒子为中心，以光速向四周发散运动，光子其实是静止在空间中随空间一同运动。

光子的粒子性，是因为光子由激发电子构成，光子的波动性是空间本身的波动，空间时刻在波动，波动速度就是光速。

利用统一场论动量和能量公式，可以求出光子的动量和能量公式。

统一场论的动量方程标量形式：

\[ \begin{equation}\nonumber m\ c\ \sqrt{1 - \dfrac{v^2}{c^2}} = m'\ c \end{equation} \]

由于光子的静止质量 \(m'= 0\) ，

所以，\(m\ c\ \sqrt{1 - \dfrac{v^2}{c^2}} = 0\)

所以，\(m^2\ c^2 - m^2\ v^2 = 0\)

所以，光子运动的时候动量分为大小相等的正负两部分，使得总动量为零，其中单独一项是【标量形式】：

\[ \begin{equation}\nonumber p = m\ c^2 \end{equation} \]

点击展开修正：上式或应改为 \(p = m\ c\)

统一场论动量方程的矢量形式为：

\[ \begin{align} \overrightarrow{p_\text{静}} &= m'\ \vec{c'} \nonumber \\ \overrightarrow{p_\text{动}} &= m\ (\vec{c} - \vec{v}) \nonumber \end{align} \]

由于光子的静止质量 \(m'=0\) ，且 \(\overrightarrow{p_\text{动}}\) 和 \(\overrightarrow{p_\text{静}}\) 的数量相等，

因此导致光子的运动动量分为大小相等的正负两部分，总动量为零：

\[ \begin{align} \overrightarrow{p_\text{动}} = m\ (&\vec{c} - \vec{v}) = \vec{0} \nonumber \\ m\ \vec{c} &= m\ \vec{v} \nonumber \end{align} \]

两边除以 \(m\) ，得到 \(\vec{c} = \vec{v}\)

这个就解释了光子在静止质量为零为什么一定要以光速运动。

以上光子动量公式，其中单独一项是【矢量形式】：

\[ \begin{equation}\nonumber \vec{p} = m\ \vec{c} \end{equation} \]

由统一场论能量方程 \(E = m'\ c^2 = m\ c^2\ \sqrt{1 - \dfrac{v^2}{c^2}}\) 和光子的静止质量 \(m'=0\) ，得到：

\[ \begin{equation}\nonumber m'\ c^2 = m\ c^2\ \sqrt{1 - \dfrac{v^2}{c^2}} = 0 \end{equation} \]

光子的静止能量为零，运动能量分为大小相等的正负两部分，总的能量也是零：

\[ \begin{align} m\ c^2\ \sqrt{1 - \dfrac{v^2}{c^2}} &= 0 \nonumber \\ m^2\ c^2\ c^2 - m^2\ c^2\ v^2 &= 0 \nonumber \end{align} \]

其中单独一项为：

\[ \begin{equation}\nonumber E = m\ c^2 \end{equation} \]

按照以上的推理，我们把光子的能量方程 \(E = m\ c^2\) 除以光速 \(c\) 得到光子的动量方程：

\[ \begin{equation}\nonumber p = m\ c \end{equation} \]

矢量式为

\[ \begin{equation}\nonumber \vec{p} = m\ \vec{c} \end{equation} \]

光子的动量 \(p\) 和能量 \(E\) 满足以下关系：

\[ \begin{equation}\nonumber p = \dfrac{E}{c} \end{equation} \]

对于光子，可以看出统一场论给出的能量公式和相对论有相同部分，也有不同部分。

光子的静止质量为零，因而其静止能量 \(m'\ c^2\) 也是零，而光子的运动总的能量 \(m\ c^2\ \sqrt{1 - \dfrac{v^2}{c^2}}\) 也是零，所以光子的运动速度 \(v = c\)

光子运动能量分为正负两部分，其中任意一部分都是 \(m\ c^2\) ，所以，光子运动的时候，其运动能量也可以表示为 \(E = m\ c^2\)

以上表明，光子仍然遵守能量守恒。

我们可以设计一个试验，来证明光子其实就是激发电子。

设想一个机械持续带动一个发电机不停地发电，给一个灯泡供电，灯泡不断的向外界辐射光子，如果光子是灯丝中电子激发的，最终会使灯泡灯丝中的电子枯竭。

这个试验的难点就是如何屏蔽外界的空气，给灯丝及线路补充损耗的电子。